Using the battery in the simulation
Variables to be defined
System (external) point of view
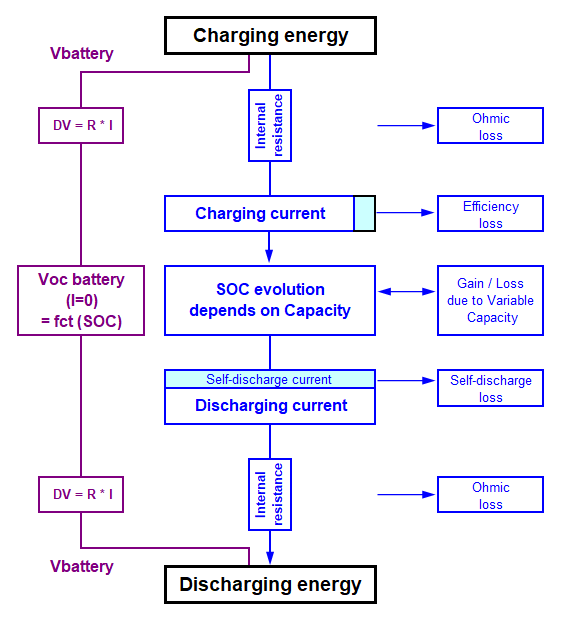
When using a battery in the simulation, we are interested in:
- The charging energy ECharge,
- The discharging energy EDischarge,
- The variation of internal energy ESOCBalance,
- The possible losses (internal resistance, faradic efficiency, self-discharge, capacity variations).
Additionnally, if the control is done in terms of:
- SOC, we have to evaluate the State of Charge SOC. This is specific to the simulation, i.e. always a calculated quantity. In the reality, the SOC is not a measurable quantity; control devices using the SOC as criteria should use sophisticated means for this evaluation (historic currents balance, voltage at limits).
- Voltage thresholds, we should evaluate the battery voltage VBattery with accuracy.
Now the difficulty is that these values are not static during a time step (hour). At a given instant the system is either charging or discharging, and therefore the SOC, as well as the voltage, vary along the hour. If a control threshold is attained during the evolution within the hour, we have to change the operating mode for the rest of the hour.
Internal operation (current balance)
Within the battery, the relevant variable is the current balance (i.e. the battery "stores" electrons, indirectly an energy). The current in the battery may be either positive (charging) or negative (discharging). There cannot be a simultaneous charging and discharging mode.
The heart of the battery pack is the stored energy - or more exactly the stored current [Ah] - related to the SOC. However this is not an absolute quantity as the capacity may change according to the conditions (see below). Therefore we only deal with energy or current variations: the corresponding variable will be named ISOCBalance or ESOCBalance.
The charging current ICharge is calculated as the ECharge / VBattery. The discharging current IDisCharge is calculated as the EDischarge / VBattery. The current balance IBattery is the difference between ICharge and IDischarge (may be on a given period of time): IBattery = ICharge - IDischarge
The SOC evolution is evaluated for a specified period, according to the charge or discharge current (without losses for now): \(SOCend = SOCbeg + (IBatttery[A] * DTime [h]) / Capacity [Ah]\).
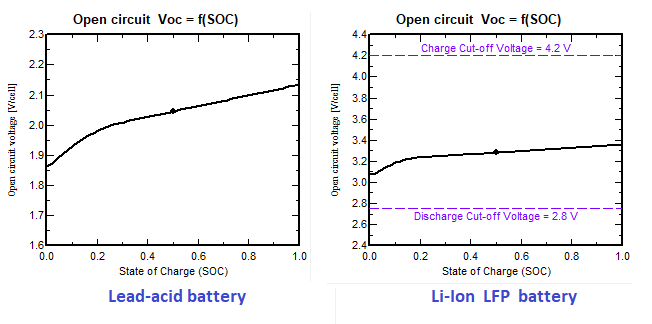
Now the internal "virtual" battery voltage (Voc, open circuit voltage without current) is defined by the battery model: it is supposed to be linear with the SOC, with a nominal voltage and a slope.
We talk here about the "normal" operating range of the battery. The behaviors at extremities will be discussed later.
Therefore the stored/restored energy is calculated as
\(ESOCbalance [Wh] = (SOCend - SOCbeg) * Capacity [Ah] * VBattery [V]\)
Losses in normal operation
There are several sources of losses:
- The internal resistance ResInt acts on the VBattery value, identically when charging and when discharging: \(VBattery = VOCBattery (SOC) + ResInt * IBattery\)
- The Faradic or Coulonbic efficiency (i.e. the charge/discharge current balance) named EfficI is applied to the SOC calculation when charging; the above equation becomes, when charging: \(SOCend = SOCbeg + (IBatttery[A] * EfficI) * DTime [h]) / Capacity [Ah]\) The corresponding current loss is named IBEffL in PVsyst.
- The self-discharge, permanent slight discharging current, named IBSelf in PVsyst, dependent on the temperature.
Capacity
The battery capacity is not constant, it is indeed a function of the Charging/Discharging rate (or current), the temperature, the battery wear state.
The battery capacity current dependency is especially important with lead-acid batteries. At C100 (charge in 100 hours, i.e. ICharge = Capacity/100), the capacity may be about 40% higher than at C10. This variation is much less pronounced with Li-Ion batteries (about 4%).
Effects of capacity variability
The SOC variation is closely related to the present capacity, and this has an effect on the ISOCBalance, and therefore the stored energy and the apparent charge/discharge efficiency. Please see Battery efficiency for details, especially the last paragraph "Capacity variability".
Variable names in PVsyst simulation
When you want to analyse detailed simulation data, the variables names in PVsyst are simplified. For exemple: ECharge is named EBatCh, EDischarge is EBatDis, ESOCBalance is ESOCBal, the battery voltages are named U_Batt, UBatCh, UBatDis, etc. Within an hour, you can have simultaneous values EBatCh and EBatDis, as the operating status may have changed along the hour. The operating times will be given by ChargeON and DischON. The effective capacity used for the concerned hour is also available as an hourly variable. NB: During the simulation, the losses are not stored as energies, but as currents: IBEffL, IBSelf, IBGass. Therefore the energy evaluation for the annual loss has to be done with an average battery voltage.
High and low charging conditions
The behaviour at the "extremities" of the operating range are not mentioned in this schema, but correctly accounted for during the simulation. Please see Battery overcharging for details, especially Overcharging losses and Deep discharge losses.