|
<< Click to Display Table of Contents >> Temperature behaviour correction |
  
|
|
<< Click to Display Table of Contents >> Temperature behaviour correction |
  
|
In the standard one-diode model, the temperature behavior is essentially determined by the dependency of the diode saturation current Io:
Io(T) = Io ref ( Tc / Tc ref )3 · exp [ ( q · EGap / Gamma · k) · ( 1 / Tc ref - 1 / Tc ) ]
i.e. with a cubic and exponential temperature dependency, as well as a dependency on the Egap and Diode Ideality factor Gamma.
This expression fixes the muVco and muPmax temperature coefficient values, which are therefore a result of the model.
Temperature Correction on Gamma
Remember that the Gamma value (diode ideality factor) is one of the 5 unknown parameters of the one-diode model, determined (or supposed) in correlation with the Rserie choice, which can vary from 0 to Rsmax.
The muVco and muPmax resulting from the model are not necessarily the same as the manufacturer's specifications. Therefore PVsyst allows for modifying the temperature behavior of the model by introducing a linear variation of Gamma with operating Temperature:
Gamma = Gamma0 + muGamma * (Tmod - Tref)
In the PV module definition dialog, page "Model parameters" / "Temper coeff.", the user may specify a required muPmpp value, and PVsyst will determine the suited "muGamma" correction factor.
For crystalline modules, the model represents quite well the reality, so that the correction is usually very low (rarely above 0.03 - 0.04%/°C).
With the amorphous and other thin film technologies, the temperature coefficient is very sensitive to the d2MuTau parameter. According to our detailed measurements, cumulating this correction with the recombination leads to degraded performances of the model (that is, its ability to reproduce the data in any conditions). However when defining parameters for such modules in the database, this parameter is used for a final fit o the specified muPmpp value and may be up to 0.12%.
NB1: The tool shows a graph of the induced variations on muVoc, muVmpp and muPmpp. According to the one-diode model, the muVco and muPmax coefficients are not constant, they vary themselves with the temperature. Therefore applying the manufacturer's values established for 25°C as constant derate factors is not necessarily correct.
NB2: The curves may sometimes show a broken behavior at very low temperatures. This is due to a computation limitation: as you see in the above expression, the temperature dependency of the Io is very important. With some modern modules (very good fill factors), the IoRef value at 25°C becomes very low, and the exponential leads to pA fractions for which we had to put a lower limit. This break corresponds to the computational limit.
muVco temperature coefficient
Externally specified muVco and muPmax temperature coefficients cannot be reproduced simultaneously by the one-diode model. When we adjust muGamma for getting the required muPmax behavior, the muVco is fixed, not necessarily to the value specified by the manufacturer.
A correct (or specified) Vco behaviour as function of the temperature is not really necessary during the simulation: no energy is produced at Vco !
However the coefficient muVco is used during the system sizing, for the determination of the Maximum voltage potentially attainable by the PV Array under worst conditions (i.e. lower temperatures even encountered). This safety test is required during the design of the PV array, and the PVsyst value (from the model) sometimes leads to higher Voc(Tmin) than some designing software using the specified muVco.
This is the reason why the PVsyst database now allows to store the muVco value specified by the manufacturer (only available for some few modules in the present time). And in the project's definition (button "Project's Settings"), you can choose to use this value instead of the PVsyst value during your design.
Details about the muPmpp determination
According to the measurements reported by the specialized laboratories, the maximum power point Pmpp behaves very linearly with the temperature.
The muPmpp parameter specified by the manufacturers is the slope of this linear dependence.
Now the Pmpp temperature dependency as calculated by the one-diode model is not exactly linear:
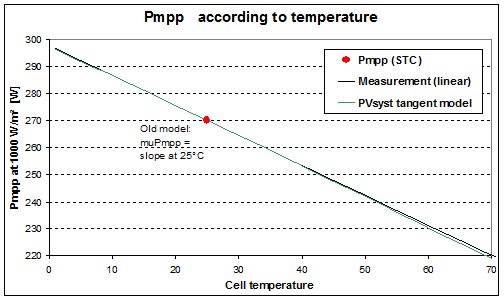
When this little discrepancy is not really visible here, we may draw a plot with a zoom on the real behaviour:
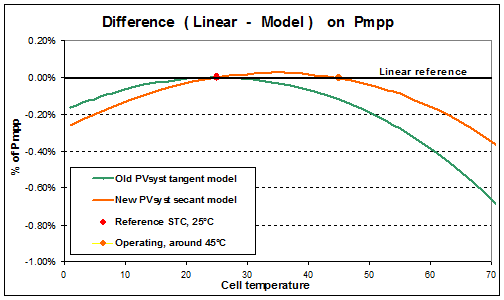
Until Version 6.25, PVsyst adjusted the slope for getting the correct slope at 25°C (i.e. a tangent adjustment). In these conditions the derive is around -0.03% at 35°C, -0.12% at 45°C and -0.28% at 55°C with respect to the linear hypothesis.
Since the version 6.26, PVsyst chooses the slope corresponding to the secant between 25°C and 45°C. This improves the accuracy of the model at the real operating temperatures, and results in a diminution of the temperature loss of about -0.1 to -0.2% (of annual yield) with usual PV systems (depending on the climate and the thermal U-factor).